Dilution Theory – Page 1:Dilution Plating |
|
||||
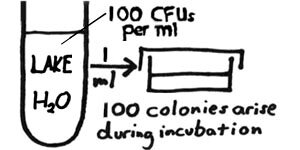
In quantitative microbiology, we are concerned with determining the concentration of colony-forming units (CFUs) in our sample – i.e., the number of CFUs per ml or per gram of the sample. For example, if we were to plate out one ml of a lake water sample and then – after incubation of the plates – find that 100 colonies have arisen, we would then conclude that there were 100 CFUs per ml of the lake water. More realistically (as with most of our area lakes), the concentration of CFUs in the water could have been considerably greater. Counting the colonies on a plate inoculated with one ml of water may be impossible. We would like to have "countable" plates – containing between 30 and 300 colonies. If fewer than 30, we run into greater statistical inaccuracy. If greater than 300, the colonies would be tedious to count and also would tend to run together. |
||
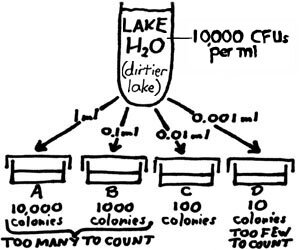
We may try to plate out smaller and smaller amounts, as in the example shown at right. With this new lake water sample, a countable plate (Plate C: 100 colonies) is achieved with the inoculation of 0.01 ml of sample. Figuring out the number of CFUs per ml of the sample would go like this: Whatever the number of CFUs in the inoculum of Plate C (one-hundreth of a ml of the sample), there would be one hundred times as many CFUs in one ml of the sample. So, if 100 CFUs are determined to be in the 0.01 ml inoculum, then 100 X 100 CFUs would be present in one ml; the final answer is 10,000 CFUs/ml of the sample. Two drawbacks to this procedure: It is difficult with our equipment to dispense amounts smaller than 0.1 ml. Also, the smaller the amount tested, the less representative it is of the sample. |
||
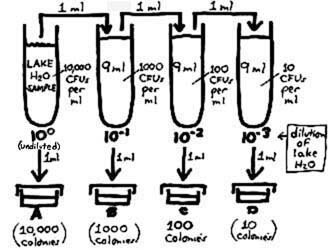
So we now get into "dilution theory" to accomplish the equivalent of plating out succeedingly smaller amounts of sample. Making serial decimal dilutions (i.e., successive 1/10 dilutions, each made by adding one part of inoculum to 9 parts of diluent) and inoculating one ml into each of the plates, we can construct a plating procedure (shown at right) that is equivalent to the above. Note that for each 1/10 dilution, we are taking one part of inoculum and spreading it out over a total of 10 parts; the concentration of organisms thereby becomes one-tenth as dense. Illustrating further how the concentration of CFUs decreases according to how these cell suspensions are diluted: We determined above that the sample contains 10,000 CFUs per ml. Taking out one ml and inoculating it into a 9 ml dilution blank (the second tube) would put the 10,000 CFUs into a total of 10 ml which is equivalent to 1000 CFUs per ml of the 1/10 dilution of the sample. The density of CFUs continues to decrease ten-fold with each subsequent dilution. Counting 100 colonies in Plate C, note how we can work back to a concentration of 10,000 CFUs per ml of the sample. So, by inoculating 1 ml of a 10–2 dilution into the plate which is subsequently counted, we are theoretically doing the equivalent of plating 10–2 ml (i.e., 0.01 ml) of the lake water sample. (Scientific notation is reviewed here.)
Compare the solution just obtained with the previous solution where Plate C was inoculated with 0.01 ml of sample:
|